(1×) Semantic Security
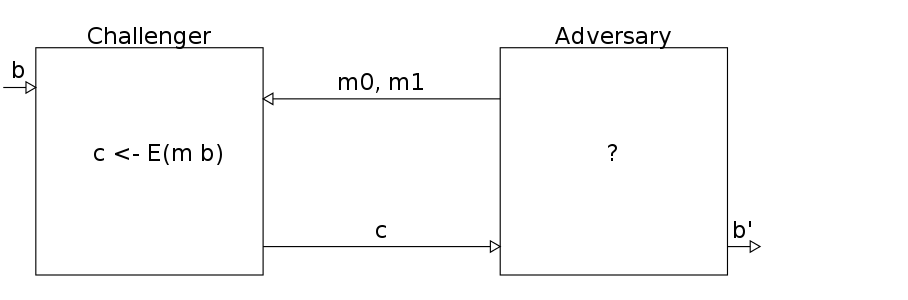
advantageSS G = | Pr[G 0 ≡ 1] - Pr[G 1 ≡ 1] |Encryption E is semantically secure iff forall "efficient" adversary A, advantageSS (E ⇆ A) is "negligible".
`Bits : ℕ → `Set
`Bits = `Vec `Bit
|M| |C| |R| : ℕ -- Parameters
M = `Bits |M| -- The message space
C = `Bits |C| -- The cipher-text space
R = `Bits |R| -- Randomness needed to encrypt
Enc = M `× R `→ C -- Encryption
E : Enc -- Parameter
advantageSS G = | Pr[G 0 ≡ 1] - Pr[G 1 ≡ 1] |Encryption E is semantically secure iff forall "efficient" adversary A, advantageSS (E ⇆ A) is "negligible".
Rₐ = Bits |Rₐ| -- Adv′s randomness
-- AdvCont = Rₐ → (M × M) × (C → Bit)
Adv = (Rₐ `→ M `× M)
× (Rₐ `× C `→ Bit)
_⇆_ : Enc → Adv → Bit → Rₐ × R → Bit
(E ⇆ (A₀ , A₁)) b (rₐ , r) = d
where
m = A₀ rₐ
c = E (m b , r)
d = A₁ (rₐ , c)EncTr = Enc → Enc
AdvTr = Adv → Adv
encTr : EncTr
advTr : AdvTr
⟨E⟩ = encTr E
⟨A⟩ = advTr A
advantageSS (⟨E⟩ ⇆ A) ≈ advantageSS (E ⇆ ⟨A⟩)record Universe (`Set : Set) : Set where
constructor mk
field
`⊤ : `Set
`Bit : `Set
_`×_ : `Set → `Set → `Set
`Vec : `Set → ℕ → `Set
`Bits = `Vec `BitSet-U : Universe Set
Set-U = mk ⊤ Bit _×_ Vec
Bits-U : Universe ℕ
Bits-U = mk 0 1 _+_ (flip _*_)
Fin-U : Universe ℕ
Fin-U = mk 1 2 _*_ _^_
⊤-U : Universe ⊤
⊤-U = _ -- Agda figures out that there
-- is only one such universerecord FunUniverse (`Set : Set) : Set₁ where
constructor _,_
field
universe : Universe `Set
_`→_ : `Set → `Set → Set
i `→ᵇ o = `Bits i `→ `Bits o
`Endo A = A `→ AagdaFunU : FunUniverse Set
agdaFunU = Set-U , λ A B → A → B
bitsFunU : FunUniverse ℕ
bitsFunU = Bits-U , λ i o → Bits i → Bits o
finFunU : FunUniverse ℕ
finFunU = Fin-U , λ i o → Fin i → Fin o
constFunU : Set → FunUniverse ⊤
constFunU A = ⊤-U , λ _ _ → A
circuitFunU : FunUniverse ℕ
circuitFunU = Bits-U , _⌥_data _⌥_ : ℕ → ℕ → Set where
rewire : ∀ {i o} → (Fin o → Fin i) → i ⌥ o
-- cost: 0 time, o space
_∘_ : ∀ {m n o} → n ⌥ o → m ⌥ n → m ⌥ o
-- cost: sum time and space
<_×_> : ∀ {m n o p} →
m ⌥ o → n ⌥ p → (m + n) ⌥ (o + p)
-- cost: max time and sum space
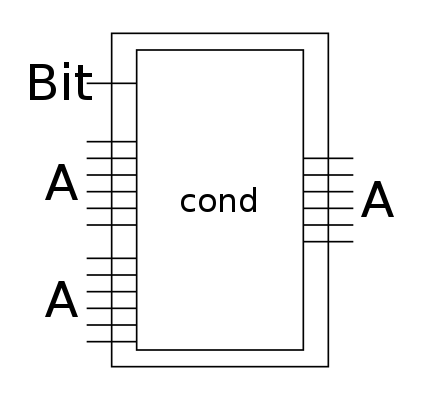
cond : ∀ {n} → (1 + (n + n)) ⌥ n
-- cost: 1 time, 1 space
bits : ∀ {n _⊤} → Bits n → _⊤ ⌥ n
-- cost: 0 time, n space
xor : ∀ {n} → Bits n → n ⌥ n
-- cost: 1 time, n space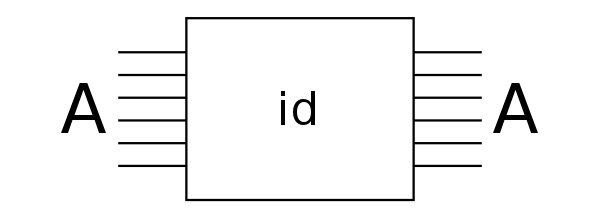
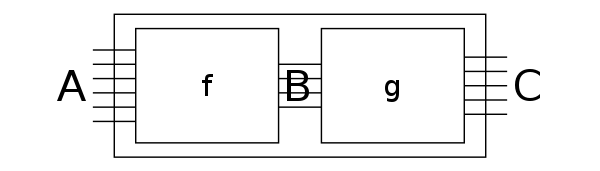
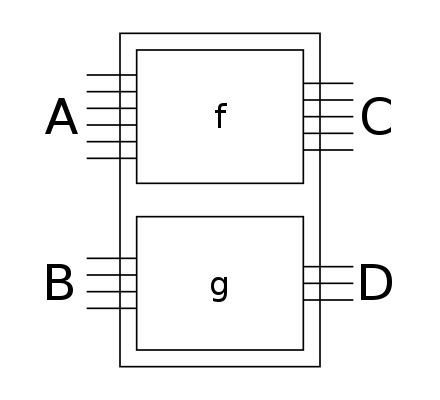
record FunPack : Set₁ where
field
`Set : Set
funU : FunUniverse `Set
funO : FunOps funUTime = ℕ
timeCostModel : FunPack
timeCostModel = record
{ `Set = Time
; funU = constFunU Time
; funO = record { rewire = const 0
; _∘_ = _+_
; <_×_> = _⊔_
; cond = 1
; bits = const 0
; xor = const 1 } }Space = ℕ
spaceCostModel : FunPack
spaceCostModel = record
{ `Set = Space
; funU = constFunU Space
; funO = record { rewire = λ {i} {o} _ → o
; _∘_ = _+_
; <_×_> = _+_
; cond = 1
; bits = λ {n} _ → n
; xor = λ {n} _ → n } }AdvTr = ∀ (fp : FunPack) → Adv fp → Adv fpagdaFunPackspaceCostModel and timeCostModelcircuitPack