BREACH

Agda

• A dependently typed functional programming language:
  • Functions are dependently types
  • Pure (side effect-free)
  • Exhaustively defined
  • Guaranteed to terminate
• A proof assistant for a powerful logic:
  • A unified environment for proofs and programs
  • Curry Howard:
    • Propositions as Types
    • Proofs as Programs
  • Backed by Computational Content:
    • Witnesses are constructed
    • No axiomatization required

Why Crypto?

Privacy is a critical issue!

Proofs should be fully verified!

Why Agda?

• Functional programming everywhere:
  • Exploration functions: summations & brute-force
  • Persistent data by default
  • Functions are deterministic and exhaustive by default
  • Processes are expressed by pure functions
• Dependent types everywhere:
  • Precise types for machines and humans
  • Convenient in the code
  • Pervasive in the proofs
• Type theory everywhere:
  • Type isomorphisms on Σ-types to prove equality on sums
  • Protocols as a type-universe
  • Process type as a decoding of protocols
  • Randomized function & Probabilistic reasoning

Public Key Encryption

• Each participant generates a key pair:
  • The private-key sk is kept secret and never disclosed
  • The public-key pk is widely distributed in association with user′s identity
• Alice wants to send a private message m to Bob:
  • Alice obtains Bob′s public-key
  • Encryption Enc pk m produces a cipher-text c
  • Alice sends c to Bob
  • Decryption Dec sk c re-produces the message m
  • Only Bob knows his private key and thus message was private

Security notions

• IND-CPA: Indistinguishability under chosen-plaintext attack

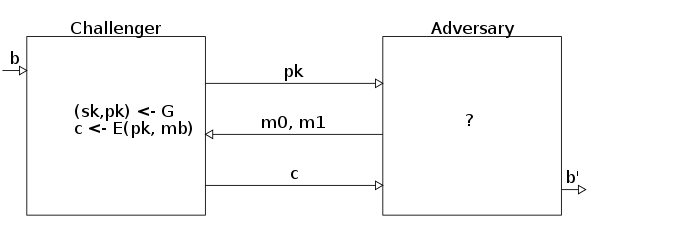
 AdversaryAdvantage A  =  | Pr[IND-CPA b A ≡ b] - 1/2 |

Agda type for IND-CPA adversaries

-- The IND-CPA adversary comes in two parts
record Adversary : ★ where
  field
    -- In the step 'm', the adversary receives some
    -- randomness, the public key.
    -- The adversary returns the message (m₀ and m₁).
    m  : Rₐ → PubKey → Message ²

    -- In the step 'b′' the adversary receives the same
    -- randomness supply and public key as in step 'm'
    -- and receives the ciphertext computed by the
    -- challenger. The adversary has to guess which
    -- message (m₀ or m₁) has been encrypted.
    b′ : Rₐ → PubKey → CipherText → Bit

Deterministic Encryption

Attack:

module Det-Enc-Attack (rₐ : Rₐ) (pk : PubKey) where
  m : Message ²
  -- m₀ and m₁ have to be different

  b′ : CipherText → Bit
  b′ c = c == Enc pk m₁ …

Proof sketch:

b′ (Enc pk (m b) …)
  ≡ Enc pk (m b) … == Enc pk m₁ …
  ≡ b == 1
  ≡ b

Randomness is paramount

• How to defeat this attack? Encryption should be randomized (hence non-deterministic)!
• The function Enc actually takes an extra parameter containing the necessary randomness.
• Textbook RSA encryption: RSA-Enc (e,n) m = mᵉ [mod n].
• Is RSA insecure?

IND-CPA attack game

-- The game step by step:
-- (pk) key-generation, only the public-key is needed
-- (mb) send randomness, public-key and bit
--      receive which message to encrypt
-- (c)  encrypt the message
-- (b′) send randomness, public-key and ciphertext
--      receive the guess from the adversary
EXP : Bit → Adversary → R → Bit
EXP b A (rₐ , rₖ , rₑ) = res
  where
  module A = Adversary A
  pk  = proj₁ (KeyGen rₖ)
  mb  = A.m rₐ pk b
  c   = Enc pk mb rₑ
  res = A.b′ rₐ pk c

game : Adversary → (Bit × R) → Bit
game A (b , r) = b == EXP b A r

Size Leak

Attack:

module Size-Leak-Attack (rₐ : Rₑ) (pk : PubKey) where
  m : Message ²
  -- m₀ and m₁ have to be of a different size

  b′ : CipherText → Bit
  b′ c = size c == size (Enc pk m₁ rₐ)

Proof sketch:

b′ (Enc pk (m b) rₑ)
  ≡ size (Enc pk (m b) rₑ) == size (Enc pk m₁ rₐ)
  ≡ size (m b) == size m₁
  ≡ b == 1
  ≡ b

Size matters

IND-CPA actually requires the two messages to be of the same size!

Compression AFTER Encryption?

Useless!
Compression after encryption is fruitless, since encrypted data looks like random, and random can't be well compressed.

Encryption AFTER Compression = ♥ ?

      CEnc : PubKey → Message → Rₑ → CipherText
      CEnc pk m rₑ = Enc pk (compress m) rₑ
 

Brök3n‼

Compression Oracle

Attack:

module Compression-Oracle (rₐ : Rₐ) (pk : PubKey) where
  m : Message ²
  -- m₀ and m₁ have to be of the same size while
  -- compress to a different size

  b′ : CipherText → Bit
  b′ c = size c == size (CEnc pk m₁ rₐ)

Proof sketch:

b′ (CEnc pk (m b) rₑ)
  ≡ size (CEnc pk (m b) rₑ) == size (CEnc pk m₁ rₐ)
  ≡ size (Enc pk (compress (m b)) rₑ)
      ==
    size (Enc pk (compress m₁) rₐ)
  ≡ size (compress (m b)) == size (compress m₁)
  ≡ b == 1
  ≡ b

Compression side-channel attack

• Assume any compression scheme, which:
  • Can map two messages of the same size to compressed messages of different size.
• Assume any encryption scheme, which:
  • Is IND-CPA secure.
  • Leaks the size of the plain-text message.
  • Cipher text size does not depend on the randomness.

CRIME

At ekoparty 2012, Thai Duong and Juliano Rizzo announced CRIME, a compression side-channel attack against HTTPS. An attacker with the ability to:

• Inject partial chosen plaintext into a victim's requests
• Measure the size of encrypted traffic

can leverage information leaked by compression to recover targeted parts of the plaintext.

BREACH

BREACH (Angelo Prado, Neal Harris, Yoel Gluck) is a category of vulnerabilities and not a specific instance affecting a specific piece of software. To be vulnerable, a web application must:

• Be served from a server that uses HTTP-level compression
• Reflect user-input in HTTP response bodies
• Reflect a secret (such as a CSRF token) in HTTP response bodies

BREACH Overview

GET /owa/?ae=Item&t=IPM.Note&a=New&id=canary=<guess>

<span id=requestUrl>https://malbot.net:443/owa/forms/
    basic/BasicEditMessage.aspx?ae=Item&amp;t=IPM.Note&
    amp;a=New&amp;id=canary=<guess></span>
...
<td nowrap id="tdErrLgf"><a href="logoff.owa?
    canary=d634cda866f14c73ac135ae858c0d894">Log Off</a></td>

(example from the paper on BREACH)

BREACH setup

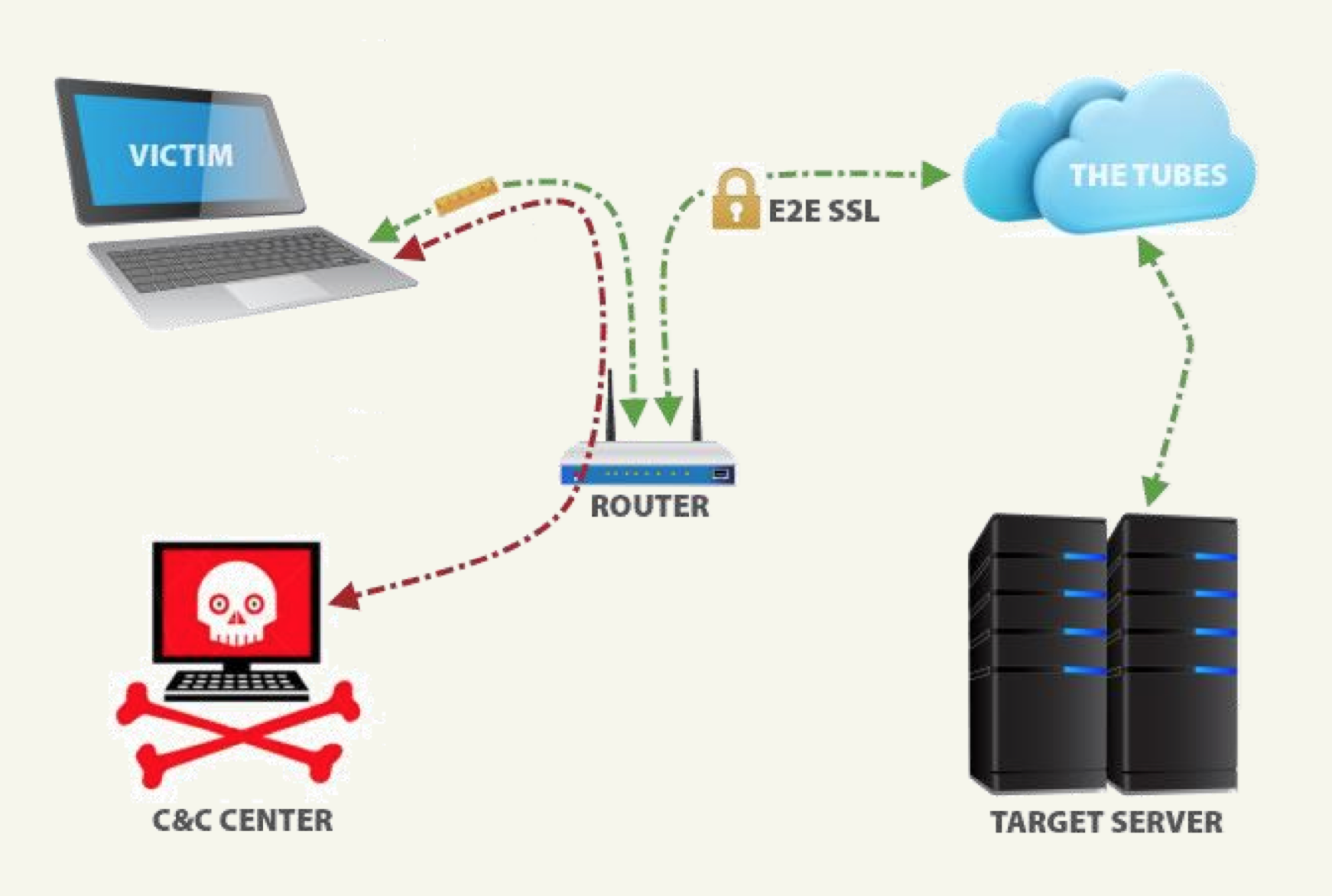
(picture from the paper on BREACH)

BREACH in Agda: mockup

Byte = Vec Byte

module BREACH M {{MonM : Monad M}}
  (doQuery      : ∀ {n} → Bytes n → M Response)
  {-
   doQuery guess =
    sendQuery
     (Enc pk (… ++ "canary=" ++ encodeGuess guess ++ …))
  -}
  (exploreByte  : Explore Byte)
  (findMinimumM : ∀ {A} → Explore A → (A → M ℕ) → M A)
  (iterateM     : ∀ {A : ℕ → Set}
                    (f : ∀ {m} → A m → M (A (suc m)))
                    (n : ℕ) → M (A n)) where
  open Monad MonM

  guessOneByte : ∀ {n} → Bytes n → M (Bytes (suc n))
  guessOneByte guess =
    (_∷ʳ_ guess) <$>
      findMinimumM exploreByte λ b →
        size <$> doQuery (guess ∷ʳ b)

  result : ∀ {n} → M (Bytes n)
  result = iterateM {Bytes} guessOneByte _
 

BREACH, Technical Challenges

Technical Challenges, met and overcame by BREACH:

• Huffman Coding and the Two-Tries Method
• Block ciphers
• Guess Windows
• Encoding Issues
• False Negatives and Dynamic Padding
• False Positives and Looking Ahead

My mockup does not address any of those, yet.

Future work

• Verifying voting schemes: Helios, Prêt-à-Voter, Mixnets...
• And the required dependencies:
  • Homomorphic encryption
  • Non-interactive Zero-knowledge proofs (NIZK)
  • Naor-Young transform (IND-CPA+NIZK → IND-CCA2)
  • ...